0%

用 JavaScript 实现八大排序

发表于 更新于 分类于 阅读次数： 79
本文字数： 11k 阅读时长 ≈ 10 分钟

八大排序分别是 冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序、基数排序。本文介绍这八大排序算法的基本思想和过程，并尝试使用 JavaScript 实现它们。

各个排序的复杂度如下表所示：

排序 平均情况 最好情况 最坏情况 辅助空间 稳定性
冒泡排序 O(n^2) O(n) O(n^2) O(1) 稳定
选择排序 O(n^2) O(n^2) O(n^2) O(1) 不稳定
插入排序 O(n^2) O(n) O(n^2) O(1) 稳定
希尔排序 O(n^1.3) O(n logn) O(n^2) O(1) 不稳定
快速排序 O(n logn) O(n logn) O(n^2) O(n logn) 不稳定
归并排序 O(n logn) O(n logn) O(n logn) O(n) 稳定
堆排序 O(n logn) O(n logn) O(n logn) O(1) 不稳定
基数排序 O(d(n+r)) O(d(n+r)) O(d(n+rd)) O(n+rd) 稳定

0 JavaScript 自带排序

即 Array.prototype.sort()，原理为插入排序与快速排序混合。sort 会改变原数组，并返回排序后的数组（不过一般没人使用其返回值）。

注意，sort 不含参数时，默认是按 字母顺序 对数组进行升序排序。

1
2
3
4
5
6
7
let fruits = ["banana", "apple", "orange", "mongo"];
fruits.sort();
console.log(fruits);	// [ 'apple', 'banana', 'mongo', 'orange' ]

let nums = [40, 100, 1, 5, 25, 10];
nums.sort();
console.log(nums);	// [ 1, 10, 100, 25, 40, 5 ]

为使结果按数字顺序进行排序，sort 接受一个 回调函数 作为参数，如下所示：

1
function(a, b) {return a - b;}

可以直接简写为箭头函数：

1
(a, b) => a - b

回调函数的两个参数代表数组中准备比较的两个值，并根据返回值决定排序：

  1. 返回值为负值，将 a 向前排
  2. 返回值为正值，将 b 向前排
  3. 返回值为零，a、b 顺序不变

因此，可以为回调函数填写不同的返回值，以进行不同的排序方式。

1
2
3
4
5
6
7
8
9
let nums = [40, 100, 1, 5, 25, 10];
nums.sort((a, b) => a - b);	// 数字升序排序
console.log(nums);	// [ 1, 5, 10, 25, 40, 100 ]
nums.sort((a, b) => b - a);	// 数字降序排序
console.log(nums);	// [ 100, 40, 25, 10, 5, 1 ]

let students = [{id: 1, scores: 85}, {id: 2, scores: 90}, {id: 3, scores: 82}];
students.sort((a, b) => a.scores - b.scores);	// 按每个元素的scores属性升序排序
console.log(students);	// [ { id: 3, scores: 82 }, { id: 1, scores: 85 }, { id: 2, scores: 90 } ]

注意回调函数的返回值是数值，而非布尔值，不要写成 (a, b) => a < b。

1 冒泡排序（Bubble Sort）

典型的排序算法。两个数两两比较大小，大数后移（下沉），小数前移（冒泡）。

这里用一个大小为 2 的窗口，每次从后往前滑动比较，直到最小的数被顶到最前。紧接着对后面 n - 1 个数进行同样的操作，直至比较完毕。

一共进行 n - 1 趟比较，第 i 趟（i 从 0 开始）对 n - i 个数进行 n - i - 1 次比较，每趟结束后有一个数被排好位置，因此复杂度为 O(n^2)。

1
2
3
4
5
6
7
8
9
10
11
function bubbleSort(arr) {
  const final = [...arr], n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    for (let j = n - 1; j > i; j--) {
      if (final[j - 1] > final[j]) {
        [final[j - 1], final[j]] = [final[j], final[j - 1]];
      }
    }
  }
  return final;
}

优化： n - 1 趟比较需要全部完成，如果某趟比较已经完成排序，则进行了多余的遍历。

可以设置标志位 flag，表示本趟比较 是否进行了冒泡交换，如果一趟下来都没有进行冒泡交换，表示元素已经有序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function bubbleSort(arr) {
  const final = [...arr], n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    let flag = false;
    for (let j = n - 1; j > i; j--) {
      if (final[j - 1] > final[j]) {
        [final[j - 1], final[j]] = [final[j], final[j - 1]];
        flag = true;
      }
    }
    if (!flag) {
      break;
    }
  }
  return final;
}

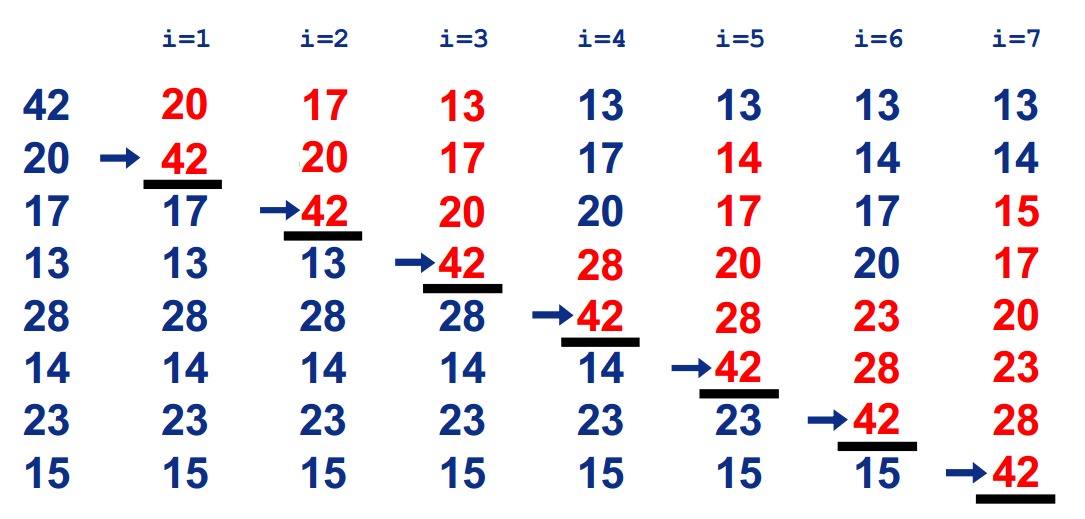
2 选择排序（Selection Sort）

找数组中元素的最小值，并顶到最前，然后在后面剩下的元素中重复操作。

第 i 次（i 从 0 开始）遍历，在后面 n - i 个数中找出最小值，与第 i 个元素交换并固定下来，一共进行 n - 1 次遍历，每次遍历有一个数被排好位置，因此复杂度为 O(n^2)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function selectionSort(arr) {
  const final = [...arr], n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < n; j++) {
      if (final[j] < final[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex !== i) {
      [final[i], final[minIndex]] = [final[minIndex], final[i]];
    }
  }
  return final;
}

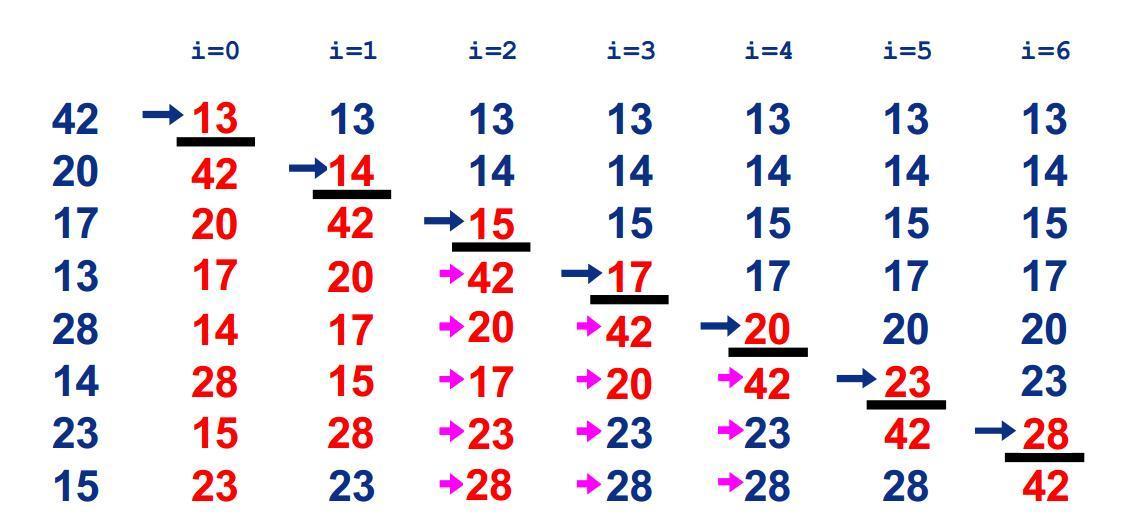
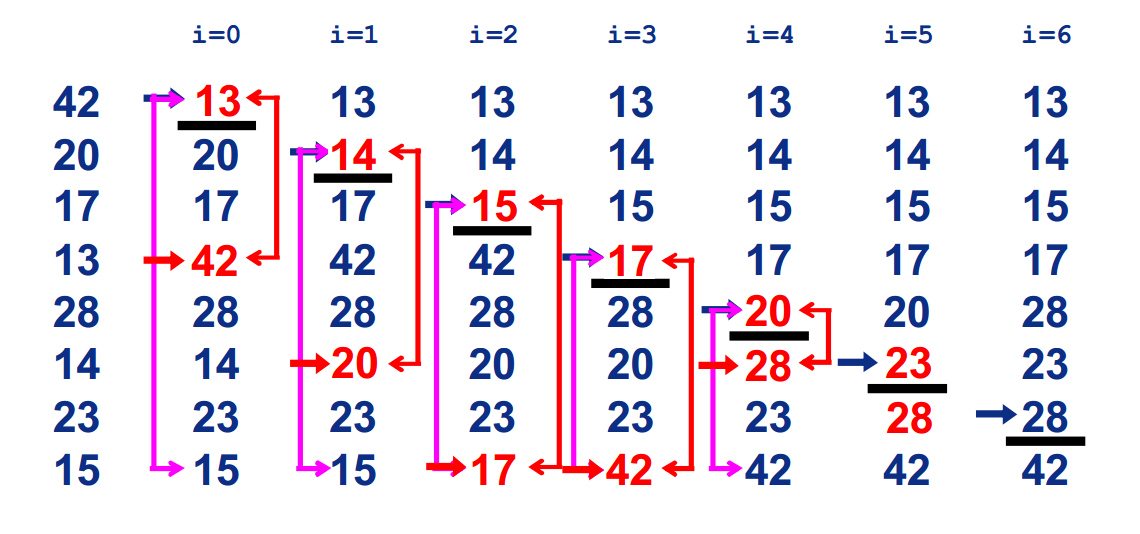
3 插入排序（Insertion Sort）

类似于 插扑克牌排序，在一个已经排好序的序列中，插入一个新的数，使得新序列依然有序。

每次插入一个数，一共插入 n 次。第 i 次（i 从 0 开始）插入下标为 i 的数时，为比较数组前 i + 1 个数的大小，需要对这 i + 1 个数进行一遍冒泡排序。因此复杂度为 O(n^2)。

代码实现时，下标为 0 的数默认已插入，且不需要比较，i 可以从 1 开始循环；此外，冒泡排序时，由于元素是有序的，从后往前找插入位置时，找到后即可进入下一轮遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
function insertionSort(arr) {
  const final = [...arr], n = arr.length;
  for (let i = 1; i < n; i++) {
    for (let j = i; j > 0; j--) {
      if (final[j - 1] > final[j]) {
        [final[j - 1], final[j]] = [final[j], final[j - 1]];
      } else {
        break;
      }
    }
  }
  return final;
}

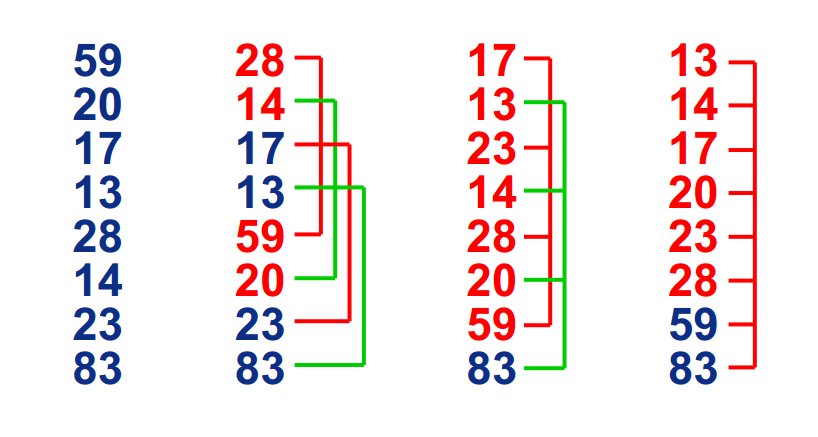
4 希尔排序（Shell Sort）

当数列 基本排好序 时，使用插入排序会更高效。因此可以分步长成子序列，对每个子序列做插入排序。

基本思路是，设置初始步长为数组长度的一半，将数组分为若干个子数组，子数组个数即为步长数。对每个子数组做插入排序，过程同上。依次缩小步长，直至步长为 1，此时数组经过插入排序后已经完全排序。

时间复杂度为 O(n^1.3-2)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function shellSort(arr) {
  const final = [...arr], n = arr.length;
  let increment = n;
  while (true) {
    increment = Math.floor(increment / 2);
    // 一共有increment个子数组，起始下标从0到increment-1
    for (let k = 0; k < increment; k++) {
      // 以下是插入排序
      for (let i = k + increment; i < n; i += increment) {
        for (let j = i; j > k; j -= increment) {
          if (final[j - increment] > final[j]) {
            [final[j - increment], final[j]] = [final[j], final[j - increment]];
          } else {
            break;
          }
        }
      }
    }
    if (increment === 1) {
      break;
    }
  }
  return final;
}

5 快速排序（Quick Sort）

快排 yyds！基本思想是 分治（分而治之），从数列中选出一个 key 值，并让其他数分边站（小于往左，大于等于往右），在左右两边重复这一步骤，直至区间长度为 1。

如何让数分边站？需要用到 挖坑填数 的方法。

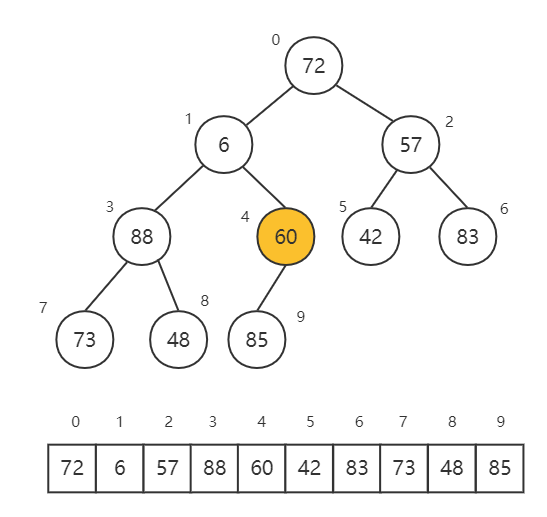
  • 设这样的一个数组：[72, 6, 57, 88, 60, 42, 83, 73, 48, 85]，初始时，设 i = 0，j = 9，key 选取第一个数 a[0] = 72。
  • a[0] 被选走后，相当于 a[0] 出现了一个空洞，我们从后往前（j--）找出一个比 key 小的数，发现 j = 8，a[8] = 48 满足这个条件，将 a[8] 填到 a[0] 中。
  • 这时 a[8] 又形成了空洞，我们从前往后（i++）找出一个比 key 大的数，发现 i = 3，a[3] = 88 满足这个条件，将 a[3] 填到 a[8] 中。
  • 这一轮结束后，i = 3，j = 7，key = 72。再重复上述操作，先从后往前找，再从前往后找。如下一轮，找到 j = 5，a[5] = 42，将 a[5] 填到 a[3] 中；找到 i = 5，此时 i === j，退出。
  • 再将 key = 72 填到最后的空洞 a[5] 中，此时数组为：[48, 6, 57, 42, 60, 72, 83, 73, 88, 85]，可以看出 a[5] = 72 前面的数都大于它，后面的数都小于它。再对 a[0...4] 和 a[6...9] 重复上述步骤即可。

这个过程重复 n 次，每次对数组对半分，复杂度为 O(n logn)。

key 有多种选择方法，如中间数或随机数，会影响算法复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function quickSort(arr) {
  const final = [...arr], n = arr.length;
  sorting(0, n - 1);
  return final;

  function sorting(left, right) {
    if (left >= right) {
      return;
    }
    let i = left, j = right;
    const key = final[left];
    while (i < j) {
      while (i < j && final[j] >= key) {	// 从右往左找第一个小于key的值
        j--;
      }
      if (i < j) {
        final[i] = final[j];
        i++;
      }
      while (i < j && final[i] < key) {	// 从左往右找第一个大于key的值
        i++;
      }
      if (i < j) {
        final[j] = final[i];
        j--;
      }
    }
    // 此时i === j
    final[i] = key;
    sorting(left, i - 1);	// 对左子区间递归调用
    sorting(i + 1, right);	// 对右子区间递归调用
  }
}

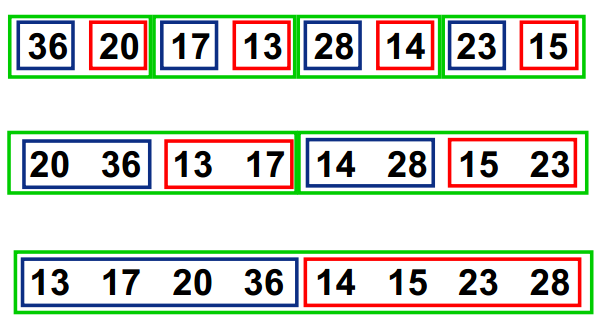
6 归并排序（Merge Sort）

基本思想同样是 分治。通过归并若干个已经排好序的子序列，达到整个序列完成排序的目的。

首先考虑，如何 合并两个有序数列？可以比较两个数列的第一个数，然后取出较小的一个，并在原数列删除该数，再重复操作，如果一个数列已空，依次取出另一个数列的元素即可。代码实现时，不用实际删除，可以用指针移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function test(a, b) {
  const m = a.length, n = b.length;
  const c = new Array(m + n);
  let i = 0, j = 0, k = 0;
  while (i < m && j < n) {
    if (a[i] < b[j]) {
      c[k++] = a[i++];
    } else {
      c[k++] = b[j++];
    }
  }
  while (i < m) {
    c[k++] = a[i++];
  }
  while (j < n) {
    c[k++] = b[j++];
  }
  return c;
}

根据上面的思想，如果数组分成两组 A、B 且这两组有序，就可以方便地合并。

如何使 A、B 有序？将 A、B 各自再分成两组，以此类推，直到小组内只有 1 个数据时，视为小组有序，再合并相邻的两个小组即可。也就是 先递归分解数列，再合并数列。

将数列分开小数列需要 logn 步，每一步合并有序数列需要 O(n)，总的时间复杂度为 O(n logn)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function mergeSort(arr) {
  const final = [...arr], n = arr.length;
  sorting(0, n - 1);
  return final;

  function sorting(left, right) {
    if (left < right) {
      let middle = Math.floor((left + right) / 2);
      sorting(left, middle);	// 对左子区间递归调用
      sorting(middle + 1, right);	// 对右子区间递归调用
      mergeArray(left, middle, right);	// 归并左右子区间
    }
  }

  function mergeArray(left, middle, right) {
    let i = left, m = middle, j = middle + 1, n = right;
    let k = 0;
    const temp = new Array(right - left + 1);
    while (i <= m && j <= n) {
      if (final[i] < final[j]) {
        temp[k++] = final[i++];
      } else {
        temp[k++] = final[j++];
      }
    }
    while (i <= m) {
      temp[k++] = final[i++];
    }
    while (j <= n) {
      temp[k++] = final[j++];
    }
    for (let ii = 0; ii < k; ii++) {
      final[left + ii] = temp[ii];
    }
  }
}

7 堆排序（Heap Sort）

首先，了解什么是 堆 和 最小堆，以及 shiftDown 操作。堆是用完全二叉树结构（只有二叉结构，且都在左边）存储数据的结构，也称二叉堆。最小堆是指堆中某个节点值不小于其父节点的值，因此最顶端总为最小值。

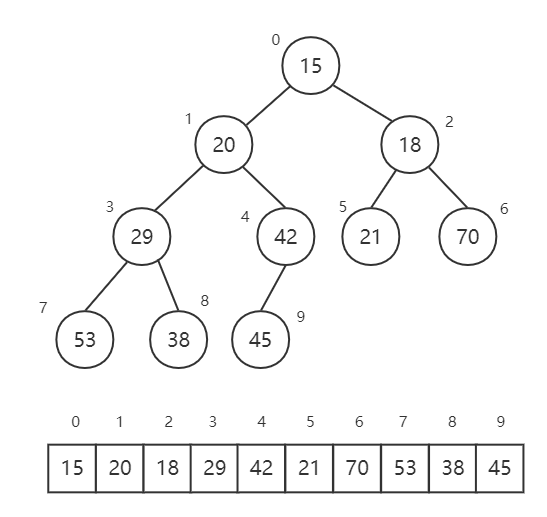
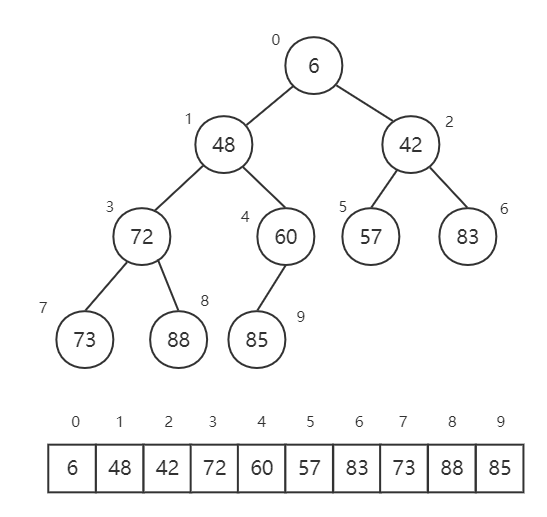
下图是一个最小堆，堆顶是最小值，每个节点都不小于其父节点。并且可以按照图中所示顺序（从左到右，从上到下），确定每个节点的下标。

发现规律：对当前节点下标 i，有：

  • 父元素在数组中的下标为：Math.floor((i - 1) / 2)
  • 左子元素在数组中的下标为：2 * i + 1
  • 右子元素在数组中的下标为：2 * i + 2

shiftDown 操作是指对于一个堆的根节点，判断其与子节点的大小关系。如果该节点更大，则不满足最小堆定义，此时该节点与子节点互换（下移）。重复这个操作，直到该节点找到它的位置（不再大于其两个子节点）。

接下来介绍堆排序。堆排序的思想是，构造一个 最小堆，然后 依次取出堆顶最小值，直到堆为空。

首先构造最小堆。对于已有的数组，可以按下标顺序转换为这样一个二叉树。然后，我们找到最后一个含有子节点的节点，这个节点应是最后一个节点 n - 1 的父节点，根据上面的规律，其下标是 Math.floor((n - 2) / 2)。

从后往前遍历，对每个有子节点的节点，都把其当做根节点，对 其下面的完全二叉树 做 shiftDown 操作（这个过程称为建立堆的调整），直到整个二叉堆满足最小堆，最小堆构造完成。

构造完成后，数组并非排好序，因为堆只满足父子节点的大小关系。为此，我们需要依次取出最小值，每次重复取出，直至堆为空。

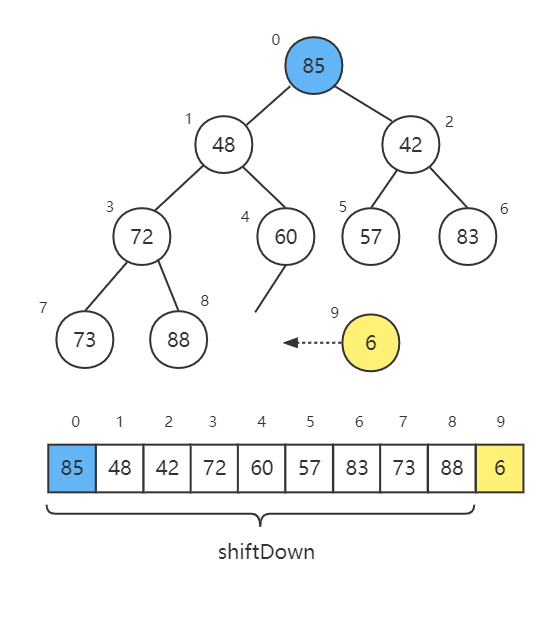
堆中只能取出最大优先级的元素，即根节点，最小堆的根节点就是最小值。取出最小值后，会在堆顶形成空洞，这时需要把数组最后一个元素放到堆顶（根节点），然后对新的根节点进行 shiftDown 操作（这个过程称为最小堆的恢复）。

代码实现时，我们可以将设置 shiftDown 的操作范围，对于已经放到末尾的最小值，shiftDown 时不再处理它。

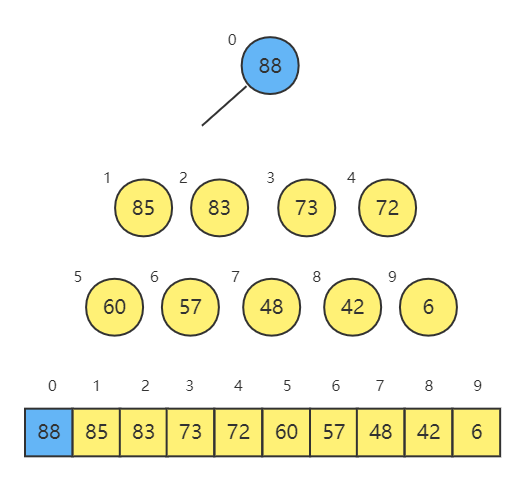
最终得到的数组是降序排序的数组，为了得到升序排序，我们对其 reverse 即可。

每次恢复堆的时间复杂度为 O(logn)，共 n - 1 次恢复堆操作，建立堆时也需要调整 n / 2 次，每次 O(logn)，总的时间复杂度为 O(n logn)。

参考：基础堆排序 | 菜鸟教程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function heapSort(arr) {
  const final = [...arr], n = arr.length;
  makeMinHeap();	// 构造最小堆
  for (let i = n - 1; i > 0; i--) {
    [final[0], final[i]] = [final[i], final[0]];	// 将最小值放到队尾，队尾填补堆顶
    minHeapShiftDown(0, i);	// 堆顶元素做shiftDown，为了不影响队尾最小值，设置i为最后子节点位置（不包括i）
  }
  return final.reverse();	// 将降序数组反转为升序数组

  function makeMinHeap() {
    // 构造最小堆，从后往前对有子节点的节点做shiftDown
    for (let i = Math.floor((n - 2) / 2); i >= 0; i--) {
      minHeapShiftDown(i, n);
    }
  }

  function minHeapShiftDown (i, n) {
    // i是需要shiftDown的根节点位置，n是最后一个子节点的位置（不包括n）
    let j = 2 * i + 1;  // 找左子节点位置
    while (j < n) {
      if (j + 1 < n && final[j] > final[j + 1]) {
        j++;	// 在左右节点中找较小值
      }
      if (final[i] <= final[j]) {
        break;	// 如果父节点小于等于子节点，则该节点有效，无需下移
      }
      [final[i], final[j]] = [final[j], final[i]];	// 节点下移
      i = j;
      j = 2 * i + 1;
    }
  }
}

8 基数排序（Radix Sort）

首先，了解什么是 桶排序（Bin Sort，又称箱排序、计数排序）。

最基础的桶排序创建一个大小为 max + 1 的数组 count（max 为原数组的最大数字）用来存储每个数字的个数，初始值记为 0，然后做两轮遍历：

  1. 遍历原数组 nums，将数字对应下标的计数值加 1，即 count[num]++，这一轮复杂度为 O(n)
  2. 遍历计数数组 count，将不为 0 的下标值输出，这一轮复杂度为 O(max)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function binSort(arr) {
  const final = [...arr], n = arr.length;
  const count = new Array(Math.max(...final) + 1).fill(0);
  for (const num of final) {
    count[num]++;
  }
  let k = 0;
  for (let i = 0; i < count.length; i++) {
    for (let j = 0; j < count[i]; j++) {
      final[k++] = i;
    }
  }
  return final;
}

这样的桶排序有一定的问题：如果数组中有负数，就没有对应下标；或者最小值远大于 0，此时前面的空间都被浪费了。

优化的桶排序： 找出最小值 min 和最大值 max，计数数组长度为 max - min + 1，下标也进行偏移，下标为 i 的元素对原数组中的 i + min 进行计数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function binSort(arr) {
  const final = [...arr], n = arr.length;
  const min = Math.min(...final), max = Math.max(...final);
  const count = new Array(Math.max(max - min + 1)).fill(0);
  for (const num of final) {
    count[num - min]++;
  }
  let k = 0;
  for (let i = 0; i < count.length; i++) {
    for (let j = 0; j < count[i]; j++) {
      final[k++] = i + min;
    }
  }
  return final;
}

由于上述桶排序利用 count 存储原数组的数值信息，丢失了原数组的其他信息（如两个相同数值输出的结果是不稳定的），实际操作中，还会将数组 count中的计数改为前缀和，用来快速获得每个元素值的下标（排名）。

这里推荐在获取下标时，从后往前遍历，这样对于相同值的元素，其顺序与原数组保持一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function binSort(arr) {
  const final = [...arr], n = arr.length;
  const min = Math.min(...final), max = Math.max(...final);
  const count = new Array(Math.max(max - min + 1)).fill(0);
  for (const num of final) {
    count[num - min]++;
  }
  for (let i = 1; i < count.length; i++) {
    count[i] += count[i - 1];	// 前缀和，其含义是小于等于当前数的个数
  }
  const temp = new Array(n);
  for (let i = n - 1; i >= 0; i--) {	// 从后往前遍历保证排序稳定性
    count[final[i] - min]--;	// 获取下标
    temp[count[final[i] - min]] = final[i];	// 赋值
  }
  for (let i = 0; i < n; i++) {
    final[i] = temp[i];
  }
  return final;
}

桶排序的时间复杂度为 O(n + max - min)，空间复杂度为 O(max - min)。本质上，这是一种拿空间换时间的做法，有时可以达到线性复杂度，优于快排。

可以看出，如果 max - min 较大，就会浪费过多的时间和空间。

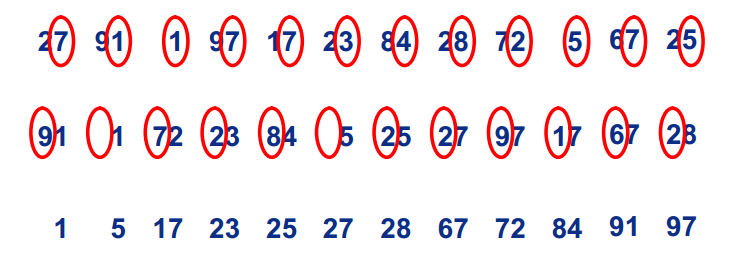
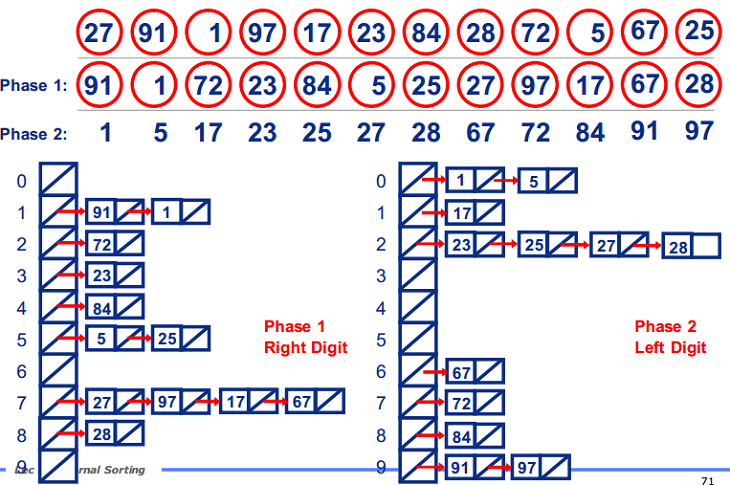
基数排序是在桶排序的基础上，通过 基数的限制 来减小开销。

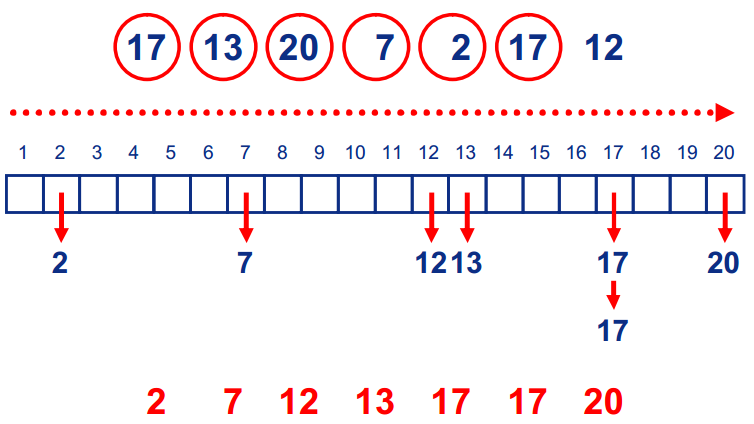
如下图所示，确定基数为 10，数组长度就为 10，每个数会在这 10 个数中寻找位置。对于某个数如 34，不会像桶排序一样把其放在下标 34 中，而是将其分成 3 和 4，第一轮排序将其放在下标 4处，第二轮排序将其放在下标 3 处。

如何确定排序轮数？排序轮数也就是数组最大值的位数，即 log(r) max + 1向下取整。代码实现时，如果某一轮排序所有数字均计数在第 0 位，表明已经完成排序。

复杂度为 O(d(n+r))，d 为排序轮数，n 为数组长度，r 为基数大小，d = log(r) max + 1 向下取整。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function radixSort(arr, r) {
  const final = [...arr], n = arr.length;
  r = r === undefined ? 10 : r;
  const count = new Array(r).fill(0);
  for (let i = 0, round = 1; ; i++, round *= r) {
    count.fill(0);
    // 计数
    for (const num of final) {
      count[Math.floor(num / round) % r]++;
    }
    // 确定位数，如果所有数字均计数在第0位，表明当前round已经超过最大值
    if (count[0] === n) {
      break;
    }
    // 处理为前缀和
    for (let j = 1; j < r; j++) {
      count[j] = count[j - 1] + count[j];
    }
    const temp = new Array(n);
    // 倒序取出元素，前缀和的值就表示排序后元素的下标位置
    for (let j = n - 1; j >= 0; j--) {
      count[Math.floor(final[j] / round) % r]--;
      temp[count[Math.floor(final[j] / round) % r]] = final[j];
    }
    for (let j = 0; j < n; j++) {
      final[j] = temp[j];
    }
  }
  return final;
}

Reference

  1. JavaScript 数组排序
  2. 排序算法总结 | 菜鸟教程
  3. 用typescript实现八大排序-递增 - Kingfish404
  4. 堆的基本存储 | 菜鸟教程

Gitalk 加载中 ...